Келли Л. Росс (Kelley L. Ross).
 Онтология и космология неевклидовой геометрии
Онтология и космология неевклидовой геометрии
Хотя в природе никогда не было круга или треугольника,
истины, продемонстрированные Евклидом, навсегда сохранят свою достоверность и
очевидность.
Дэвид Юм (David Hume), An Enquiry Concerning Human Understanding, Section IV, Part I, p. 20 [L.A. Shelby-Bigge, editor, Oxford University Press, 1902, 1972, p. 25]
#1. Введение
До недавнего времени то, что Альберт Эйнштейн жаловался в свои поздние годы
по поводу вразумительности квантовой механики, философы и физики часто не
принимали всерьез, относясь к нему, как к старому чудаку, впавшему в маразм. К
счастью, это дело сейчас заканчивается, поскольку философы и математики калибра
Карла Поппера и Роджера Пенроуза явно указывают на остающиеся концептуальные
сложности квантовой теории [см. Penrose's searching discussion in The
Emperor's New Mind, chapter 6, "Quantum magic and quantum
mystery," Oxford 1990]. Парадокс
кошки Шредингера теперь уже иногда представляют не как замечательное и
потрясающее следствие из теории, а так, как это было изначально: аргумент “reductio ad absurdum” (доведения до абсурда) против “новой” квантовой
механики Гейзенберга и Бора. Шредингер разделял опасения Эйнштейна и других.
Чудесное утверждение по поводу всего этого можно найти в предисловии
Джозефа Агасси к недавно вышедшему “Einstein Versus Bohr” диссидентствующего физика Менделя Сачса (Mendel Sachs) (Open Court, 1991):
Когда я был студентом-физиком, меня
обеспокоили сложности, представленные и обрисованные в книге Сачса. И физики, и
философы науки, которым я признавался в своей обеспокоенности, - так ясно, как
только мог, - оказывали мне скорее враждебность, чем симпатию. Ранее я
испытывал то же самое со стороны моих преподавателей религии, так что
враждебность меня не сломила, но у меня ослабло желание следовать моим научным
интересам. Эта книга вернула меня в те дни и напомнила о той огромной
радости, которую я испытывал тогда,
читая Эйнштейна и Шредингера и встречаясь с Карлом Поппером и Альфредом Ланде.
Все четверо выражали, тем или иным путем, то же отношение, что и Сачс: надо
поощрять, а не препятствовать мыслям о сложностях в новых идеях.
Удивительно, что такие вещи приходится говорить, и весьма показательно
то, что ответы, которые Агасси получил на свои вопросы, напомнили ему
нетерпимость религиозного догматизма.
Тем не менее, достаточно редко говорится и о философской
вразумительности теории самого Эйнштейна – релятивистской теории гравитации.
Эта теория основывается на использовании неевклидовой геометрии. По поводу
последней все еще есть немало хороших вопросов; но при ее трактовке и в
популярном изложении, и в философской дискуссии, эти вопросы, если быть
последовательными, похоже, так и не были заданы. Хорошим примером этого могут
быть две статьи, опубликованные в Scientific American в 1976 году. В
статье J.J.Callahan’а, “The Curvature
of Space in a Finite Universe”, опубликованной в августе, утверждается, что
Риманова геометрия положительно искривленного, конечного и неограниченного
пространства, которую Эйнштейн использовал в своей теории, разрешает Кантовский
парадокс антиномии пространства, уходя одновременно и от конечного
пространства, и от бесконечного, в их традиционном понимании. Именно аспект
удовлетворительности теории Эйнштейна с точки зрения философии явно продолжает
оказывать влияние на современных физиков вроде Стефана Хокинса, что можно
увидеть в недавней Brief
History of Time [в интернете есть русский перевод]. С другой
стороны, в марте 1976 года Scientific American также опубликовал статью J.Richard Gott III (et al.),
“Will the Universe Expand Forever”? В
этой статье были детально рассмотрены свидетельства того, что вселенная не
положительно искривлена, конечна и неограничена, как Эйнштейн, да и все после
него, хотели. Напротив, вселенная скорее всего неограничена, либо с
неевклидовой геометрией Лобачевского, либо даже вообще с евклидовой (!)
геометрией.
В данный момент я не собираюсь показывать, что научная теория
переменчива. Обычно это так. Вопрос, который я затрагиваю, состоит в том, что
философский взгляд на вероятность того, что наблюдения продолжат открывать
бесконечную вселенную (вместо “исчезнувшей массы”, “черной материи”, и .т.д.),
все еще не исследован. Влияние прозрачных следствий из основанной на
наблюдениях мартовской статьи на значимость философской августовской статьи так
и не было рассмотрено ни в одной другой статье Sc.Am., - да и нигде вообще, из того, что я видел, по
философии и не по философии. Это как если бы все поджидали, надеясь, что
“исчезнувшая масса” сама(?) обнаружится. Тем временем имеем практически заговор
молчания. Если мы, как страусы, просто не будем думать опять о встрече с
бесконечной вселенной, то этого и не произойдет. Это и с интеллектуальной, и с
философской точки зрения нечестно. Но ведь для работы именно с этой частью
проблемы большую часть времени и использовали неевклидову геометрию и связанные
с ней космологические результаты. Когда мы, казалось, совсем близко подошли к
более открытому рассмотрению этих вопросов, Стефан Ховкинс и Карл Поппер [Karl Popper, Unended Quest, Open Court, 1990; p.16] указали на то, что Эйнштейн,
не важно успешно или нет ответивший на Кантовскую Антиномию пространства, не
ответил на Антиномию времени: несмотря на десятилетия восхваления философского
откровения о конечной, но неограниченной вселенной, не было замечено, что
решение, предложенное для пространства, не проходит со временем. Философы
должны благодарить Хавкинса за то, что он прямо поставил этот вопрос.
Далее я попытаюсь задавать вопросы о неевклидовой геометрии, которые я
не заметил, чтобы часто, или вообще хоть раз, задавались бы. В части 3 я затем
вкратце попытаюсь предположить, как можно пересмотреть философские заключения
об использовании Эйнштейном геометрии в его теории гравитации.
#2. Искривленное пространство и
неевклидова геометрия.
Постулат параллельности Евклида, в его современной формулировке,
утверждает, что если на плоскости есть линия и точка не на этой линии, через
эту точку можно провести только одну линию, параллельную исходной. Джероламо
Саккери (Gerolamo Saccheri, 1667-1733) блестяще попытался доказать это при
помощи аргументации типа доведения до абсурда (т.е. от противного). Есть два
пути для противоречия постулату: в пространстве 1) нет параллельных линий (прямые линии на плоскости обязательно
встретятся, если их продлить достаточно далеко), или 2) если несколько прямых
через данную точку, параллельных исходной прямой в плоскости. Они дают
неевклидовы аксиомы. Саккери получил убедительное доказательство от противного
для первого варианта путем невинного предположения того, что прямые линии
бесконечны [cf. Jeremy Gray, Ideas of Space Euclidean,
Non-Euclidean, and Relativistic, Oxford, 1989; p. 64]. Позднее Дэвид
Гильберт (1862-1953) покажет, что такое
же доказательство сведения получится, если предположить, что среди трех точек
на прямой линии только одна может быть между двумя другими [David Hilbert and
S. Cohn-Vossen Geometry and the Imagination (Anschauliche Geometrie--better
translated Intuitive Geometry), Chelsea Publishing Company, 1952; p.
240]. Во втором случае, тем не менее, Саккери не смог получить хорошего
доказательства. А там использовалась аксиома точно такого типа, как те, с
которыми удалось построить первые неевклидовы геометрии Больяи (1802-1860) и
Лобачевскому (1792-1856).
Если под плоской поверхностью мы понимаем плоскость из прямых линий,
как понимал Евклид, то настоящие неевклидовы многообразия (т.е. области,
объемы, пространство-время, и т.д.), чтобы действительно противоречить Евклиду,
который говорил о прямых линиях, должны быть плоскими. Они не могут быть
искривлены. Прямые линии должны быть и прямыми по Евклиду, и удовлетворять
свойствам, заданным неевклидовыми аксиомами. Тем не менее, начиная с Бернарда
Римана (1826-1866), про неевклидовы многообразия говорится, что они “кривые”, и
только евклидово пространство называется “плоским”. Из противоречия #1
получается “положительно” искривленное пространство (“сферическая” или
“эллиптическая” геометрия, впервые описанная самим Риманом), а из противоречия
#2 – “отрицательно” искривленное пространство (“гиперболическую”, или
Лобачевского, геометрию). Для Евклида, это, кажется, несомненно доказывало бы
его позицию: постулат параллельности – о прямых линиях, так что использование
кривых вряд ли даст честную неевклидову геометрию. “Кривизна” в этом отношении,
тем не менее, используется в необычном смысле. “Внутренняя” кривизна отделяется
от “внешней” кривизны. Пространство может иметь “внутреннюю” кривизну, но все
же содержать линии (“геодезические”), которые будут прямыми согласно любой
форме измерения, внутренней для этого пространства. Геодезическая “пряма”
относительно ее собственного многообразия. Евклидова прямота, таким образом,
характеризует геодезию 3-х мерного пространства без внутренней кривизны, и то,
что мы называем евклидовы геодезические прямыми, - всего лишь следствие общего
соглашения. [Обратите внимание, что мои ссылки на “Евклидово” пространство
всегда будут означать 3-х мерное пространство, как это понимал сам Евклид (или
Кант). “Плоские” пространства с более, чем тремя измерениями могут называться
евклидовыми из-за отсутствия кривизны; но это расширение геометрии было бы
большой новостью для Евклида, и а бы хотел сохранить историческую связь между
“евклидовой” и Евклидом]. То, что “кривизна” могла бы значить для Евклида, -
это теперь “внешняя” кривизна: чтобы линия или плоскость была “крива”, она
должна занимать пространство более высокой размерности, т.е. кривой линии нужна
плоскость, кривой плоскости – объем, кривому объему – 4-е измерение, и т.д. К
“внутренней” кривизне более высокая размерность не имеет никакого отношения. Но
как это произошло? Почему “кривизна”
смогла получить это необычное значение? Зачем нам запутывать себя,
говоря, что “внутренние” прямые линии, геодезические, в неевклидовых
пространствах имеют кривизну?
Это произошло потому, что неевклидовы плоскости можно смоделировать как
внешне искривленные поверхности в евклидовом пространстве. Так поверхность
сферы – это классическая модель
двумерной положительно искривленной Римановой поверхности; но в то время
как большие круги – это, согласно внутренним свойствам этой поверхности, прямые
линии (геодезические), в нашем представлении эта поверхность сама искривлена по
третьему измерению евклидова пространства. С учетом того, сфера является таким
хорошим представлением неевклидовой поверхности, и сферическая тригонометрия
была хорошо развита в то время, сейчас кажется несколько удивительным, что она
не стала основой первой из созданных неевклидовых геометрий [cf. Gray ibid.
p.171]. Однако, как замечено, такая геометрия не противоречит другим аксиомам,
которые можно легко положить в основу геометрии. А признание положительно
искривленных поверхностей означает, что эти аксиомы должны быть отвергнуты.
Также, что более важно, такие модели не всегда можно успешно реализовать в
евклидовом пространстве. Самая большая проблема – с пространством Лобачевского.
Поверхность в форме седла – это пространство Лобачевского в центре седла, но
настоящее пространство Лобачевского не имеет центра. Другие модели Лобачевского
искажают формы и размеры. Не существует представления (вложения)
пространства Лобачевского, которое бы сразу все преимущества сферы: не иметь
центра, сингулярностей (т.е. точек, которые не принадлежат пространству) и
позволять перемещать фигуры с места на место без искажения формы или размера.  Трехмерные неевклидовы пространства, конечно
же, вообще нельзя моделировать, используя евклидово [в понимании автора].
Трехмерные неевклидовы пространства, конечно
же, вообще нельзя моделировать, используя евклидово [в понимании автора].
Это поднимает два вопроса: 1) что мы можем пространственно
визуализировать? (вопрос психологии) и 2) что может существовать на самом деле
(вопрос онтологии). Мы не можем представить себе настоящее пространство
Лобачевского, да и вообще любое неевклидово пространство, имеющее более двух
измерений, и никакие другие пространства, имеющие более трех измерений. Притом
мы можем представить положительно искривленную поверхность, только если она с внешней
кривизной вложена в некий объем. “Кривизна”, таким образом, была естественным
понятием для внутренних свойств потому, что для всех моделей, которые можно
визуализировать, имеется внешняя кривизна. Откуда такие ограничения на то, что
мы можем себе представить? Сейчас принято считать, что компьютерная графика
освобождает от этих ограничений, но все это относится лишь к проекциям
неевклидовой или многомерной геометрии на двумерный экран компьютера. Такие
проекции можно было с огромными усилиями делать и задолго до компьютеров; но из
этого никогда не получалось, да и не может получиться ничего больше, чем просто
плоские евклидовы рисунки кривых. Ожидание того, что такая графика может
изменить наш разум так, что мы начнем видеть вещи по-другому, - это не более
чем предсказание, или ожидание, а не факт. Поскольку к пониманию неевклидовой
геометрии мы шли почти два века, изменение нашего воображения кажется несколько
медлительным, тем не менее компьютеры могут в этом сильно помочь. Математикам
не нужно волноваться по поводу всех этих вопросов визуализации, потому что она не нужна для аналитических
формул, которые описывают пространства. Формулы наполняют смыслом неевклидовы
геометрии так, как здравый смысл никогда бы не смог.
Евклидова природа нашего воображения привела Канта к высказыванию о
том, что хотя отказ от аксиом Евклида можно принять без противоречий, наша
интуиция ограничена формой пространства, которую наш мозг налагает на мир. Хотя
было бы достаточно естественно возразить, что само существование неевклидовой
геометрии опровергает теорию Канта, такая точка зрения не учла бы значение
термина “синтетический”, заключающееся в том, что синтетическое утверждение может
быть отвергнуто без противоречий. Леонард Нельсон осознал, что Кантовская
теория подразумевает предсказание неевклидовой геометрии, а не ее отвержение, и
что существование неевклидовой геометрии подтверждает заявление Канта о том,
что аксиомы геометрии синтетические [Leonard Nelson, "Philosophy and Axiomatics,"
Socratic Method and Critical Philosophy, Dover, 1965; p.164]. Для теории Канта разумность неевклидовой
геометрии – это ни онтологический, ни психологический вопрос, а просто вопрос
логики – использование критерия возможности Юма
для логически согласованной постижимости. Что-то вроде этого признал, несколько
колеблясь, Джереми Грей:
-
Читая Канта,
вижу, что он не говорит, что неевклидова геометрия логически невозможна, но это
только потому, что он вообще не утверждает, что какая-либо геометрия логически
верна; геометрия в его понимании синтетична, а не аналитична. Вера Канта в то,
что евклидова геометрия верна потому, что об этом говорит наша интуиция,
кажется мне непонятной или неправильной. [Gray, Ibid. p. 85]
Если мы не можем представить себе неевклидовы геометрии без
использования внешне кривых линий, то, тем не менее, легко прийти к заключению
о разумности кантовкой теории. Смысл верности евклидовой геометрии для Канта –
это не больше и не меньше, чем вера сотен геометров в постулат о
параллельности, уверенность, основанная на нашем очень реальном
пространственном воображении. Если заявление Канта “непонятно”, то Грей не
объяснил, почему на протяжении истории вплоть до 19-го века все верили, что постулат
о параллельности истинен. Это психологический вопрос, не логический или
онтологический. Ощущение этой средневековой уверенности можно увидеть в любое
время и сегодня, просто пытаясь объяснить неевклидову геометрию
студентам-выпускникам, которые никогда раньше о ней не слышали. Мы могли бы
сказать, что попытки доказать постулат показывают, что он беспокоил людей; но
все подозревали, что постулат на самом деле теорема, и никто не обратил свое
беспокойство в попытку построить геометрию с отрицанием постулата. Саккери
отвергал его, но только потому, что он конструировал доказательства от
противного. Неевклидова геометрия не изменила наше пространственное
воображение, она только доказала, то, что Кант уже неявно высказал:
синтетический и аксиоматически независимый характер первых принципов геометрии.
Может быть, Кант прав и мы никогда не сможем вообразить, как выглядит
пространство Лобачевского или многомерные неевклидовы пространства, или
промоделировать их без внешней кривизны, насколько хорошо бы мы не понимали
аналитические уравнения. Это в чистом виде вопрос психологии, и совсем не
логики, математики, физики или онтологии. Математики могут спокойно
игнорировать ограничения нашего воображения, хотя они при этом рискуют так
далеко уйти от здравого смысла, что передовые рубежи математики ни коим образом
не будут доступны даже в целом много знающим людям [это уже сейчас имеет место,
автор просто этого не заметил J]. Более того, поскольку Кант верил, что
пространство – это форма, навязанная миру нашим воображением, он не верил, что
пространство существует отдельно от нашего опыта. Это приводит нас к
онтологическому вопросу: что может существовать на самом деле? Неевклидова
геометрия была не более, чем математическим курьезом до тех пор, пока Эйнштейн
не применил ее к физике. Теперь проблема, кажется, стала существенно глубже и
сложнее, чем в дни Канта или Римана. Если наше воображение неизбежно евклидово,
жестко прошитое в мозг, если проводить аналогию с компьютерами, но Эйнштейн
придумал, как применить неевклидову геометрию к миру, то мы могли бы считать,
что пространство действительно реально и имеет реальную структуру в мире вне
зависимости от того, можем ли мы визуально его себе представить.
В свете различий между внутренней и внешней кривизнами, мы должны
рассмотреть все возможные виды онтологических аксиом, которые покроют все
возможные пространства, которые могут быть описаны евклидовой и неевклидовой
геометрией. Если бы ограничения, накладываемые нашим воображением, показывали
нам свойства реального пространства, то мы должны были бы сказать, что
внутренняя кривизна, хотя и независима аналитически от внешней, может
существовать только вместе с внешней кривизной, и, таким образом, с вложением в
более высокие измерения. Это можно назвать аксиомой ортокривизны,
согласно которой не было бы настоящей неевклидовой геометрии, поскольку
неевклидова геодезия обязательно бы имела внешнюю кривизну и тогда никогда бы
не было действительно прямых линий, для которых нам нужна “ex hypothese”, противоречащая Евклиду. Геометрия
поверхности сферы использовала бы, таким образом, ортокривизну, потому
что внутренние прямые, большие круги, должны быть одновременно
визуализироваться и пониматься как кривые линии в трехмерном евклидовом
пространстве. С другой стороны, может быть, что внутренне кривые пространства
могут существовать в реальности без внешней кривизны, и, таким образом, не
будучи вложенными в большую размерность. Это можно назвать аксиомой гетерокривизны,
которая сделала бы настоящую неевклидову геометрию возможной, поскольку линии с
неевклидовыми отношениями между собой были бы прямыми в общем понимании этого
понятия по Евклиду или Канту.
Можно провести дальнейшее онтологическое разделение. В предположении,
что аксиома ортокривизны верна, возможна функционально неевклидова геометрия, если есть более высокая
размерность, разрешающая наличие внешней кривизны, существует, но скрыта от
нас. Тогда нам надо решать, существуют ли только три измерения в нашем
пространстве, или могут быть дополнительные измерения, которые мы почему-то не
чувствуем, но которые могут индуцировать внутреннюю кривизну, внешние свойства
которой не могут быть визуализированы или образно рассмотрены нами. Таким
образом, нам следует различать аксиомы закрытой ортокривизны,
утверждающая, что трехмерное пространство – это все, что есть, и открытой
ортокривизны, согласно которой более высокие размерности могут
существовать. Это дает нам три варианта:
1.
С аксиомой
закрытой ортокривизны, нет настоящих неевклидовых геометрий (и нет больше трех
пространственных измерений), есть только псевдогеометрии, состоящие из кривых в
евклидовом пространстве;
2.
С аксиомой
открытой ортокривизны, не существует настоящих неевклидовых геометрий, но мы,
возможно, имеем дело с функционально неевклидовой геометрией, внешняя кривизна
которой спрятана от нас измерениями (более трех знакомых нам пространственных
измерений), не видными нам, – а это уже очевидная гетерокривизна;
3.
Ну и с аксиомой
гетерокривизны, бывают настоящие неевклидовы геометрии, внутренние свойства
которых онтологически не подразумевают более высокие размерности (не важно,
более трех пространственных измерений существует, или нет).
Следует все время помнить, что эти аксиомы являются ответами на вопросы
по поводу реальности, которые задаются физикой или метафизикой, логически они
полностью отделены от статуса геометрии в логике или математике, и не касаются
психологических возможностей нашего воображения. Вторая аксиома оставляет
открытым вопрос о том, являются ли “скрытые” измерения просто скрытыми от
нашего восприятия, или они действительно отделены от нашего трехмерного бытия.
Держа в уме эти онтологические альтернативы, мы может перейти к рассмотрению
философских выводов из того, как Эйнштейн использовал неевклидову геометрию.
#3. Геометрия в теории
относительности Эйнштейна.
Общая теория относительности Эйнштейна предлагает считать, что “сила”
гравитации на самом деле является результатом внутренней кривизны
пространства-времени, а не Ньютоновского действия на расстоянии или
квантово-механического обмена виртуальными частицами. Если рассматривать
философскую позицию Эйнштейна как ответ на Антиномию пространства Канта, чтобы
объяснить, как прямые в пространстве могут быть конечны, но неограничены,
введение времени в качестве четвертого измерения предполагает, что мы
можем разложить кривизну пространства-времени в кривизну, основанную на
отношении между пространством и временем: мы можем думать, что теория Эйнштейна
удовлетворяет аксиоме открытой ортокривизны, с особенностью, которой на самом
деле является время, а не дополнительная размерность пространства, кроме наших
трех. Эта теория метафизически элегантна, поскольку дает нашему математическому
аппарату использовать более высокую размерность без необходимости постулировать
реально существующее пространственное измерение, выходящее за рамки нашего
опыта и нашего бытия. Время – это измерение, которое существует для нас в виде
одного пространственного слоя в каждый момент, точно так же, как третье
измерение пересекается только в одной (радиальной) точке искривленной поверхностью
сферы в нашей предыдущей модели положительно искривленного пространства [последняя аналогия автора достаточно бессмысленна, т.к.
движение сферы вдоль третьего измерения не предполагается; кажется, она даже
запутывает читателя].
Наша сферическая модель неевклидова пространства времени, тем не менее,
не совсем верна; чтобы придерживаться аналогии, внутренние прямые в
пространстве должны быть геодезическими и выглядеть прямыми для нас. Их
кривизна должна проявляться только при взгляде из более высокой размерности,
также как большие круги на сфере оказываются кривыми с нашей трехмерной
перспективы. Это не верно в смысле астрономического пространства, где пути,
описываемые свободно падающими телами в гравитационных полях весьма очевидно
искривлены для нашего трехмерного воображения, в то время как они понимаются
как геодезические в смысле их формы более размерного пространства-времени. Это
прямо противоположно случаю в нашей модели: пути свободного падения (“мировые
линии”) – геодезические в пространстве-времени, но внешне искривлены в
пространстве, в то время как большие круги модели – внешне искривленные линии в
обычном пространстве (соответствующем пространству-времени), но геодезические в
плоском пространстве (соответствующем пространству). [Этот
абзац также имеет мало собственного смысла, поскольку проекция прямой из
пространства большей размерности на искривленное подпространство меньшей
размерности, как и следует ожидать, в большинстве случаев будет кривой; на
самом деле автор просто пытается подготовить читателя к последующему тексту].
Внутренняя кривизна, введенная Риманом для объяснения того, как прямые
линии могут иметь свойства, связанные с кривизной, не будучи искривлены в
обычном смысле, теперь используется для объяснения того, как то, что очевидно
искривлено, например орбита планеты, на самом деле прямо. Что-то перевернулось
вверх ногами. Если кривизна пространства-времени очевидна для нас через внешне
искривленные линии в трехмерном пространстве, то форма аналогии заставляет нас
постулировать, что “более высокое”, или внешнее, измерение, в котором прямые
линии искривлены, как пространственное, а не временное. Если трехмерное
пространство не является внешне искривленным во время, согласно аксиоме
открытой ортокривизны, тогда получается, что это время внешне искривлено в
трехмерное пространство. В модели, где раньше поверхность сферы была аналогом
нашего пространства, теперь поверхность должна стать аналогом двумерного
пространства плюс времени, а третье измерение – тем, куда искривлены геодезические
пространства-времени. Изменение роли времени неожиданно делает модель очень
неинтуитивной, его вынуждает сделать то свойство модели, что геодезическая
находится на поверхности сферы. Это помогает в данном философском случае
отбрасыванию сложностей аксиомы открытой ортокривизны и просто принятию того,
что четыре измерения пространства-времени имеют гетерокривизну; но это упускает
из виду кантовскую Антиномию пространства, на которую мы надеемся ответить, а
также то обстоятельство, что размерность времени – не совсем такая, как
размерность пространства. Это наиболее интуитивно очевидно в формуле для
“дистанции”: Δs2 = Δt2 – (Δx2 +Δy2+Δz2)/c2. Тут формула Пифагора для изменения в пространственном положении
делится на квадрат скорости света и вычитается из квадрата изменения времени,
что дает “дистанцию” в пространстве-времени, выраженную в единицах времени.
Таким образом, время не считается просто еще одной размерностью пространства.
Поэтому нам следует рассмотреть различия между пространством и временем, и
только аксиома открытой ортокривизны позволяет это сделать.
Приписывание внешней кривизны времени также вызвано особенностями
использования одного только “кривого пространства” для объяснения гравитации,
так как это принято в музеях или книжках по всему миру; ведь кривое
пространство вызывает в воображении образы холмов и долин, через которые
движущиеся объекты описывают кривые пути. Тем не менее, такие картинки заранее
предполагают движение, а движение – это как раз то, что надо объяснить.
Гравитация не просто направляет движение – она вызывает его. Объект,
пролетающий мимо Земли, ускоряется по направлению к Земле, и, таким образом,
приобретает скорость вдоль вектора, в направлении которого до того не было
вообще никакой скорости. Объект, который оставили в состоянии покоя
относительно Земли, без начальной скорости в любом направлении, будет ускорен
по направлению к Земле. Если на тело не действуют никакие силы, то, согласно
Эйнштейну, единственное изменение, которое имеет место – это движение тела вдоль
временной; и если тело в связи с этим перемещается в пространстве, оно
должно перемещаться под действием движения вдоль этой оси. Ось времени может
перемещать объект, если она сама искривлена, так что кривизна
пространства-времени в гравитационном поле должна быть результатом кривизны
времени, а не пространства. Внешнее измерение ортокривизны, в котором прямые
линии кривы, – это измерение обычного евклидова пространства.
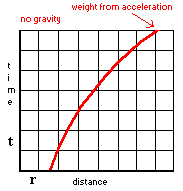 Это можно интуитивно показать не столько
нашими неевклидовыми моделями, сколько просто графиком, изображающем время (t) и одно из измерений пространства (r). Ускоренное тело опишет кривую линию, которая меняет
свою координату по оси r соответственно тому,
как меняется его координата по оси t.
Если ускорение происходит из-за самого пространства-времени, то координатная
сетка будет сама искривлена:
Это можно интуитивно показать не столько
нашими неевклидовыми моделями, сколько просто графиком, изображающем время (t) и одно из измерений пространства (r). Ускоренное тело опишет кривую линию, которая меняет
свою координату по оси r соответственно тому,
как меняется его координата по оси t.
Если ускорение происходит из-за самого пространства-времени, то координатная
сетка будет сама искривлена: 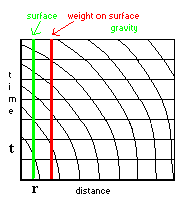 линии оси t будут кривыми, перемещая себя относительно оси r (пространственного положения), в то время как линии
оси r не будут искривляться. Кривизна самого
времени скрыта от нас, потому что, фактически, мы пересекаем только одну точку
на временной оси.
Следовательно, как мы узнаем, что нас ускоряет
гравитация?
линии оси t будут кривыми, перемещая себя относительно оси r (пространственного положения), в то время как линии
оси r не будут искривляться. Кривизна самого
времени скрыта от нас, потому что, фактически, мы пересекаем только одну точку
на временной оси.
Следовательно, как мы узнаем, что нас ускоряет
гравитация? 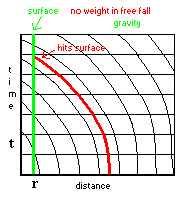 При свободном падении нас перемещает само пространство, и так мы
движемся вместе со всей нашей системой отсчета и не смогли бы определить это
локально. Действительно не можем. По принципу эквивалентности Эйнштейна, мы не
можем отличить свободное падение в гравитационном поле от свободного полета в
отсутствии оного.
При свободном падении нас перемещает само пространство, и так мы
движемся вместе со всей нашей системой отсчета и не смогли бы определить это
локально. Действительно не можем. По принципу эквивалентности Эйнштейна, мы не
можем отличить свободное падение в гравитационном поле от свободного полета в
отсутствии оного.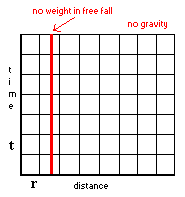 Движение, создаваемое для нас кривизной времени, видно только
потому, что мы наблюдает удаленные объекты, которые не подвержены нашему
локальному ускорению. Когда мы не падаем свободно, например стоя на поверхности Земли, мы чувствуем вес, что, согласно принципу
эквивалентности, то же самое, как если нас ускоряет некая сила (например,
двигатель ракеты), при отсутствии силы гравитации. Эти варианты действительно
эквивалентны, потому что в обоих случаях мы двигаемся относительно пространства
согласно нашей собственной системе отсчета. Когда нас ускоряет двигатель
ракеты, мы говорим, что двигаемся в стационарных координатах внешнего
пространства; но когда мы (не?) ускоряемы, стоя на поверхности Земли, то это
пространство перемещается (временем) относительно нас. Либо мы движемся сквозь
пространство, либо пространство движется через нас. Это и есть чувство веса.
Движение, создаваемое для нас кривизной времени, видно только
потому, что мы наблюдает удаленные объекты, которые не подвержены нашему
локальному ускорению. Когда мы не падаем свободно, например стоя на поверхности Земли, мы чувствуем вес, что, согласно принципу
эквивалентности, то же самое, как если нас ускоряет некая сила (например,
двигатель ракеты), при отсутствии силы гравитации. Эти варианты действительно
эквивалентны, потому что в обоих случаях мы двигаемся относительно пространства
согласно нашей собственной системе отсчета. Когда нас ускоряет двигатель
ракеты, мы говорим, что двигаемся в стационарных координатах внешнего
пространства; но когда мы (не?) ускоряемы, стоя на поверхности Земли, то это
пространство перемещается (временем) относительно нас. Либо мы движемся сквозь
пространство, либо пространство движется через нас. Это и есть чувство веса.
Остается хороший вопрос по поводу глобального характера
пространства-времени. Гравитационные поля локально положительно искривлены, но
Эйнштейн и его философские последователи явно хотели бы, чтобы все
пространство-время было положительно искривлено, т.к. конечная, но
неограниченная вселенная лучше с эстетической точки зрения, к тому же она
отвечает на кантовскую Антиномию пространства. Сейчас, однако, космологическая
геометрия пространства-времени обычно привязывается к динамической судьбе
расширяющейся вселенной. Открытые, вечно расширяющиеся вселенные относятся к
имеющим геометрию Лобачевского, или даже евклидову, и только замкнутые
вселенные, направленные к полному коллапсу, – позитивную Риманову кривизну.
Наблюдения сейчас свидетельствуют в пользу открытой вселенной, а у
“расширябельных” моделей даже есть причины предпочитать евклидову геометрию.
Эти возможности, однако, создают значительные проблемы; поскольку оба
пространства – Евклида и Лобачевского – бесконечны, и совсем разные вещи –
говорить, что Большой Взрыв бесконечной плотности начинается с конечной
сингулярности, в которую может быть упаковано конечное положительно
искривленное пространство, чем если говорить, что бесконечная гомогенная и
изотропная вселенная, которая должна быть с самого начала бесконечной,
начинается с бесконечно плотного Большого Взрыва. Сингулярность бесконечной
плотности может иметь конечную массу, а протяженная бесконечная плотность, даже
в небольшой конечной области пространства – не может.
В своей недавней статье в Scientific American, "Textures and Cosmic Structure" (March
1992), авторы, Сперджел и Турок, говорят о вселенной (они не говорят
“наблюдаемая вселенная”), начинающейся из “бесконечно малой точки”, или
вселенной, бывшей одно время размером с “грейпфрут”, как будто бы это остается
верным для всех моделей вселенных. Бесконечные вселенные даже не
рассматриваются, так что вопросы о плотности можно успешно проигнорировать.
Среди вещей, которые я видел, наиболее близок к тому, чтобы посмотреть в лицо
проблеме, абзац в “The
Matter Myth” Пола Дэвиса и
Джона Гриббина (Touchstone, 1992):
Полагаю, что бесконечность все время нас
ослепляет, и я никогда не был в состоянии построить хорошую интуитивную картину
этого понятия. Здесь имеет место составная проблема, потому что, на самом деле,
есть две конкурирующие бесконечности: есть бесконечный объем пространства, и
есть бесконечное сжатие, или компрессия, представленное сингулярностью Большого
Взрыва. Как бы вы не сжимали бесконечное пространство, оно остается
бесконечным. С другой стороны, любая конечная область в бесконечном
пространстве, сколь угодно большая, можем быть сжата в одну точку в момент
Большого Взрыва. Между двумя бесконечностями нет конфликта, пока вы указываете,
какой является та, о которой вы говорите.
В самом деле, я могу сказать все это словами,
и я знаю, что я могу придать этому математический смысл, но, признаюсь, до сего
дня я не могу визуализировать это. (с. 108).
Проблема тут, правда, не в визуализации, трудная логическая правда
состоит в том, что бесконечное пространство остается бесконечным и большой
взрыв для бесконечного пространства, хотя и может быть описан как сингулярность
по отношению к любому конечному куску пространства, не может быть конечной
сингулярностью.
Сам Эйнштейн ввел свою Космологическую константу для сохранения
статической вселенной еще до того, как Хаббл зафиксировал красное смещение. Он,
таким образом, кажется, думал, что глобальная положительной кривизны геометрия
для пространства-времени не была обязательно связана с какой-то динамической
эволюцией вселенной. Это все еще остается возможностью. Трехмерное пространство
можно понимать как имеющее врожденную гетерокривизну, не связанную с
гравитационной судьбой вселенной – неевклидово без необходимости рассматривать
время, или что-либо еще как четвертое измерение, в которое пространство должно
быть внешне искривлено. Это позволяет мыслить о конечном Большом взрыве, не
имеющем отношения к динамической судьбе вселенной, где эта судьба зависит от
эффекта кривизны времени, с локальным положительным искривлением, но глобально,
возможно, со структурой Лобачевского или Евклида. Однако, теория глобальной
гетерокривизны тогда получается стоящей отдельно от математической
релятивистской теории гравитации, и становится теорией, относящейся к
метафизической космологии в большей степени, чем к физической космологии.
Положительно гетероискривленная вселенная оказалась подходящей для
наиболее часто используемой модели всего: расширяющийся баллон, где к нашей
сферической модели неевклидовой геометрии добавляется движение. Поверхность
баллона остается сферической вне зависимости от того, будет ли баллон
надуваться вечно или ему в конечном счете будет позволено спуститься. Модель
баллона, таким образом, на самом деле постулирует пять измерений, с
поверхностью, представляющей три измерения пространства, временем в качестве
четвертого, а в качестве пятого третье(?[видимо, четвертое - пер.])
пространственное измерение, в которое наша поверхность искривлена, и через
которое поверхность движется с течением времени. Положительно
гетероискривленная вселенная, правда, не нуждается в этом пятом измерении.
Пространство было бы неевклидовым без более высоких измерений, даже с учетом
того, что оно движется вдоль временной оси, которая локально
ортоискривлена в очевидно гетероискривленное пространство-время из-за
кривизны времени. Модель баллона, таким образом, может представлять собой
теорию, отличную от той, что предполагалась, но и в наибольшей степени
наводящей на мысли, что глобальная структура изотропной и гомогенной вселенной
может позволить нам избежать бесконечного Большого Взрыва, независимого от
динамической судьбы вселенной и оправдать надежду философов на то, что Эйнштейн
разрешил кантовскую Антиномию пространства.
#4. Заключение.
Просто то, что математика работает, не означает, что мы понимаем, что
происходит в природе. Каждая физическая теория имеет математическую компоненту
и концептуальную компоненту, но их часто путают. Многие говорят, что
математическая компонента дает понимание, и это даже после десятилетий
прекрасной математики квантовой механики, которая, очевидно, не дала немного
понимания. Математика теории гравитации Ньютона была красивой и успешной на
протяжении двух веков, но не принесла никакого понимания того, чем же
была гравитация. Сейчас мы, на самом деле, имеем два различных пути понимания
гравитации, либо с помощью геометрического метода Эйнштейна, либо через
взаимодействие виртуальных частиц в квантовой механике.
Тем не менее, часто все еще есть определенное умышленное
нежелание-ничего-знать, когда утверждается, что математика – и есть объяснение.
Это не так. Напротив, каждая теория содержит концептуальную интерпретацию,
которая присваивает смысл математическим выражениям. В неевклидовой геометрии и
ее применении Эйнштейном наиболее важный концептуальный вопрос – по поводу
значения “кривизны” и онтологического статуса измерений времени-пространства,
времени, чего угодно. Наиболее важный момент – то, что онтологический статус
измерений завязан на различиях между внутренней и внешней кривизной, – это
вопрос, совершенно не связанный с математикой. Даже дальше, это вопрос,
отдельный от науки, поскольку научная теория может прекрасно работать без
необходимости решать, к чему все это с онтологической точки зрения. Некоторое
осознание этого, к сожалению, легче приводит людей к заключению о том, что
наука – это конвенционалистская или социальная конструкция, чем к более
жестокой правде о том, что по поводу реальности остается еще много непонятого,
и что философские вопросы и перспективы не всегда бесполезны и не имеют смысла.
Философия обычно плохо справляется с подготовкой путей для науки, но никогда не
было вредно задавать вопросы. Самая страшная вещь, которая когда-либо может
случиться с философией, и с наукой, это то, что люди так перепугаются всех
премудростей в областях, в которых они чувствуют свои недостатки (вроде
математики), что начнут, на самом деле, бояться задавать вопросы, которые могут
подразумевать критику, скептицизм, или, помоги им небеса, невежество.
Все эти наблюдения по поводу Относительности
Эйнштейна не являются определенными ответами ни на какие вопросы; они – просто
попытка задать вопросы, которые еще не задавались. Эти вопросы стали
возможны в связи с более ясным пониманием отдельных логических, математических,
философских и онтологических компонент теории неевклидовой геометрии.
Целью, соответственно, - поднять якорь, открыть проблемы, и взбудоражить
самоуспокоение философов, когда они думают, что кто-то другой является
экспертом и понимает вещи вполне адекватно. Работа философа как раз и состоит в
задавании вопросов и запросах, а не в принятии чьих-либо слов за чье-то еще
понимание.
#5. Эпилог, 1999г.
Затор слаженности и согласия, который раздражал меня так много лет до
написания этой статьи, да и с тех пор, возможно, сейчас ломается. Новая статься в Scientific American, "Is Space Finite?"
[Jean-Pierre Luminet, Glenn D. Starkman, & Jeffrey R. Weeks, April 1999,
pp. 90-97], в конце концов разводит геометрию вселенной и ее динамику. Подзаголовок в начале статьи говорит: “Общеизвестно,
что вселенная бесконечна” [с.90]. Правда? Это теперь “общеизвестное”? Что
Стефан Хокинг должен сказать по этому поводу? Согласно тексту: “Вопрос
конечности или бесконечности вселенной – один из старейших в философии. Обычное
заблуждение состоит в том, что уже сделан выбор в пользу второго варианта”
[с.91]. Возможно, пришло время для новой редакции A Brief History of Time!
Признавая, что плотность материи во вселенной действительно кажется
слишком низкой для того, чтобы “замкнуть” вселенную гравитационно, то есть она
динамически открыта, и, таким образом, как нам дается понять, бесконечна,
статья говорит:
Одна из проблем с этим заключением в том, что
вселенная могла бы быть сферической, но настолько большой, что наблюдаемая
часть кажется евклидовой, так же как маленький кусочек поверхности земли
кажется плоским [обычная идея в “расширябельных” теориях]. Более широкая
проблема – то, что относительность – чисто локальная теория [!]. Она
предсказывает кривизну каждой небольшой области пространства, т.е. ее
геометрию, основываясь на материи и энергии, которую она содержит. Ни
относительность, ни стандартные космологические наблюдения не говорят ничего о
том, как эти области складываются воедино во вселенную, давая ей общую форму –
топологию. [с.92, добавленные комментарии].
Так что все это время все беспокойство по поводу динамики вселенной
вообще не обязательно касалось не обязательно структуры вселенной всеобщих
масштабов. Немножко из этого в семидесятые годы было бы весьма неплохо. Если бы
Scientific American действительно опубликовал, как они могли бы, письмо, которое я написал
им в 1976 году, я был бы в замечательной позиции “Я же говорил” (хотя моей
заботой была разница, которую бы внесла дополнительная размерность, а не
топологические вопросы вроде открывшихся сейчас). Фактически, я им это говорил,
но, боюсь, это не зафиксировано в общественных архивах. Не была и эта статья
никем замечена, в частности когда она была выложена в Сеть в 1996 году. Да,
возможно, и не будет, что загасит и подавить будущие проявления энтузиазма.
Другой момент в [обсуждаемой] статье, возможно, бесполезен. Люминет и
компания говорят, что вселенная может быть конечна из-за аргумента Маха об
источнике инерции.
Возясь с причинами инерции, Ньютон представлял
себе два ведра, частично наполненные водой. Первое ведро оставляют в покое, и
поверхность воды там плоская. Второе ведро быстро вращают, и поверхность воды
вогнута. Почему?
Наивный ответ – из-за центробежной силы. Но
откуда второе ведро знает, что оно вращается? В частности, что определяет
инерциальную систему отсчета, относительно которой второе ведро вращается, а
первое – нет? Ответ Беркли [!] и Маха состоял в том, что вся материя [в которую
Беркли не верил] во вселенной сообща предоставляет систему отсчета. Первое
ведро в покое относительно отдаленных галактик, так что его поверхность
остается плоской. Второе ведро вращается относительно них же, так что его
поверхность прогибается. Если бы не было далеких галактик, не было бы причины
предпочитать одну систему отсчета другой. Поверхность обоих ведер должна была
бы оставаться плоской, и таким образом воде бы не была нужна
центростремительная сила для продолжения вращения. Короче говоря, не было бы
инерции. Мах делал вывод, что количество инерции, которую испытывает тело,
пропорционально общему количеству материи во вселенной. Бесконечная вселенная
вызывала бы бесконечную инерцию. Ничего бы никогда не смогло двигаться. [с.92, комментарии]
Каким бы ни было “наивное” объяснение, это не то, которым пользовался
Ньютон. Аргумент, высказанный Люминетом и коллегами, Беркли и Махом, на самом
деле исходно был выдвинут Лейбницем (и был просто возвращен Беркли, который
верил в пространство еще меньше, чем в материю) против Ньютоновской идеей о
том, что пространство реально.
Для Ньютона вращающееся ведра вращалось относительно самого
пространства. Очевидно, сейчас такой “общеизвестностью” считается то, что
пространство, согласно Эйнштейну, само по себе не предоставляет инерциальной
системы отсчета, поэтому никому не приходит в голову, что та как бы система
отсчета, которую пространство предоставляет при вращении, весьма отличается от
той, которую оно не может предоставить для абсолютного линейного движения
[автор почему-то не упоминает от том, как масса искривляет пространство при
вращении]. Аргумент о том, что в пустом пространстве, без “отдаленных
галактик”, не будет центробежной силы в одном ведре, и вода там будет такой же
ровной, как и в другом, не является необходимым следствием, но только лишь
теорией. Которую нелегко проверить, не имея пустой вселенной.
С другой стороны, остается вопрос, как ведро может “узнать” о том, что
“отдаленные галактики” где-то там есть. Для этого нужно физическое
взаимодействие (зона действия гравитации бесконечна); правда Эйнштейн, опять
же, сказал, что никакое физическое взаимодействие не может перемещаться быстрее
света, и в “раздувающейся” вселенной (о которой Мах даже не слышал) нас мог
достичь свет только из ограниченной части вселенной, даже в бесконечной
вселенной. Так что аргумент Люминета и др. Не работает, поскольку бесконечная
вселенная могла бы обеспечить бесконечную инерцию только если вся вселенная
могла бы физически воздействовать на данное место. Если только конечная часть
вселенной, бесконечной или нет, влияет на наше месторасположение, то была бы
все0таки конечная инерция.
 Независимо от недавней встряски в геометрии
пространства недавно в космологии был еще один сюрприз. Статья от января 1999
года, Scientific American, "Surveying Space-time with
Supernovae" [Craig J. Hogan, Robert P. Kirshner, and Nicholas B. Suntzeff,
pp. 46-51], обсуждает данные наблюдений, согласно которым расширение вселенной ускорилось
с течением времени, а не замедлилось,
как должна была бы под действием одной только гравитации. Это подразумевает
существование “космологической константы” Эйнштейна, или какой-либо другой
экзотической силы, которая бы забивала притяжение гравитации. Это также может
прояснить еще одну странность в “стандартной” космологии, которую замели под
ковер. Имеется в виду, что все замкнутые вселенные, где торможение достаточно
велико, чтобы вызвать “Большой треск”, предпочитаемые космологами вроде Стивена
Хокинга, должны были бы быть моложе, чем 2/3 Времени Хаббла (1/H). Это бы также значило, что во вселенной нет объектов,
которые могли бы иметь красное смещение больше, чем 2/3 скорости света (c), поскольку красное смещение дает нем расстояние,
пропорциональное Радиусу Хаббла (c/H), а также пропорцию возраста относительно Времени
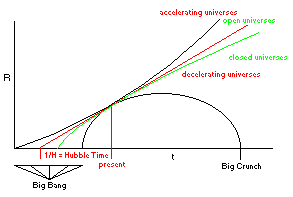
Хаббла. Таким образом, на диаграмме справа все вселенные под зеленой полосой
замкнуты, а все, что выше – открыты. Далее, многие квазары имеют красное
смещение более 2/3 c. Многие даже больше
90% c. С 70-х годов это было, на первый взгляд,
свидетельством того, что вселенная открыта, но никто более-менее влиятельный не
обратил на это внимания. Нынче, однако, вселенная ускоряется, и тогда все
возможные вселенные – над прямой красной линией на диаграмме, которая
показывает константу Хаббла. Они все будут старше Времени Хаббла. Это
неожиданно делает весьма осмысленным то, почему очень старые объекты, такие как
многие квазары, могли бы иметь очень, очень большие красные смешения.
Несомненно, , получилось бы, что сам Большой Взрыв разлетался бы быстрее, чем
скорость света – он бы имел бесконечное красное смещение. Так что нам снова
преподнесен урок по истории науки, о том, что в профессиональной науке часто
пренебрегают тщательным исследованием следствий из теории. Несоответствия могут
быть обнаружены даже при непрофессиональном исследовании.
Независимо от недавней встряски в геометрии
пространства недавно в космологии был еще один сюрприз. Статья от января 1999
года, Scientific American, "Surveying Space-time with
Supernovae" [Craig J. Hogan, Robert P. Kirshner, and Nicholas B. Suntzeff,
pp. 46-51], обсуждает данные наблюдений, согласно которым расширение вселенной ускорилось
с течением времени, а не замедлилось,
как должна была бы под действием одной только гравитации. Это подразумевает
существование “космологической константы” Эйнштейна, или какой-либо другой
экзотической силы, которая бы забивала притяжение гравитации. Это также может
прояснить еще одну странность в “стандартной” космологии, которую замели под
ковер. Имеется в виду, что все замкнутые вселенные, где торможение достаточно
велико, чтобы вызвать “Большой треск”, предпочитаемые космологами вроде Стивена
Хокинга, должны были бы быть моложе, чем 2/3 Времени Хаббла (1/H). Это бы также значило, что во вселенной нет объектов,
которые могли бы иметь красное смещение больше, чем 2/3 скорости света (c), поскольку красное смещение дает нем расстояние,
пропорциональное Радиусу Хаббла (c/H), а также пропорцию возраста относительно Времени
Хаббла. Таким образом, на диаграмме справа все вселенные под зеленой полосой
замкнуты, а все, что выше – открыты. Далее, многие квазары имеют красное
смещение более 2/3 c. Многие даже больше
90% c. С 70-х годов это было, на первый взгляд,
свидетельством того, что вселенная открыта, но никто более-менее влиятельный не
обратил на это внимания. Нынче, однако, вселенная ускоряется, и тогда все
возможные вселенные – над прямой красной линией на диаграмме, которая
показывает константу Хаббла. Они все будут старше Времени Хаббла. Это
неожиданно делает весьма осмысленным то, почему очень старые объекты, такие как
многие квазары, могли бы иметь очень, очень большие красные смешения.
Несомненно, , получилось бы, что сам Большой Взрыв разлетался бы быстрее, чем
скорость света – он бы имел бесконечное красное смещение. Так что нам снова
преподнесен урок по истории науки, о том, что в профессиональной науке часто
пренебрегают тщательным исследованием следствий из теории. Несоответствия могут
быть обнаружены даже при непрофессиональном исследовании.
Замечание по поводу цитаты под заголовком статьи:
Читателю, таким образом, дается понять, что это именно эмпирик -
“скептик” Юм, а не рационалист Кант, думает, что аксиомы геометрии
самоочевидны, Юм, который отрицает, что их истинность чем-либо обязана опыту.
Оригинал статьи:
http://www.friesian.com/curved-1.htm
Copyright (c) 1996, 1998, 1999 Kelley L. Ross, Ph.D. All Rights Reserved
Перевод (copyleft) 2002 Александр
Мельков. . Последняя версия документа: http://melkov.narod.ru/text/